- Что такое расчет ставок «корня-единицы»?
- Понимание математического ожидания
- Понимание максимального ожидаемого роста
Как наилучшим способом выбрать величину ставки после того, как игрок решит разместить ставку на рынке? Для поиска ответа на этот вопрос существует несколько распространенных методов, однако какой из них можно считать оптимальным?
Стремитесь более точно прогнозировать математическое ожидание? Дэн Абрамс углубляет метод «единицы-z» и вводит игроков на спортивных ставках в курс метода расчета ставок «корня-единицы», который позволит более эффективно и точно отыскивать преимущества при размещении ставок.
В своей недавней книге Monte Carlo or Bust (Монте-Карло или банкротство) Джозеф Бухдаль привел пример нового метода оценки ставок, который получил от него название «единица-z».
Цель метода заключается в том, что размер ставки необходимо корректировать от ставки к ставке в зависимости от коэффициентов таким образом, чтобы статистическая z-оценка оставалась неизменной. Я не буду выставлять себя на посмешище, пытаясь объяснить вам, что это означает, так что просто прочтите пояснения Джозефа, если вы еще этого не сделали.
Отличительная особенность этого нового метода заключается в следующем: при проверке его эффективности на большом наборе прибыльных футбольных ставок выяснилось, что оценочное математическое ожидание (EV), достигаемое при любых выбранных коэффициентах, оказывается куда более точным, чем при использовании более популярных методов, таких как «единица-убыток» (т. е. фиксированные ставки) и «единица-выигрыш» (т. е. ставка для выигрыша одной единицы).
Даже весьма остроумный метод «единицы-влияния» (представленный Андресом Барже-Жилем и Альфредо Гарсией-Йерно на типстерской платформе Pyckio, а затем опубликованный в Journal of Sports Economics) оказался неточным при использовании более высоких коэффициентов. Еще одним тонким местом этого метода является факт того, что формула, которую мы вывели для расчета максимального вероятного математического ожидания (или же ожидаемого преимущества), основывается на z-оценке и является весьма сложной для восприятия.
Я не буду повторять ее здесь и уберегу вас от переизбытка чересчур сложных формул. Вместо этого я воспроизведу диаграмму результатов сравнения доступного математического ожидания и десятичных коэффициентов.
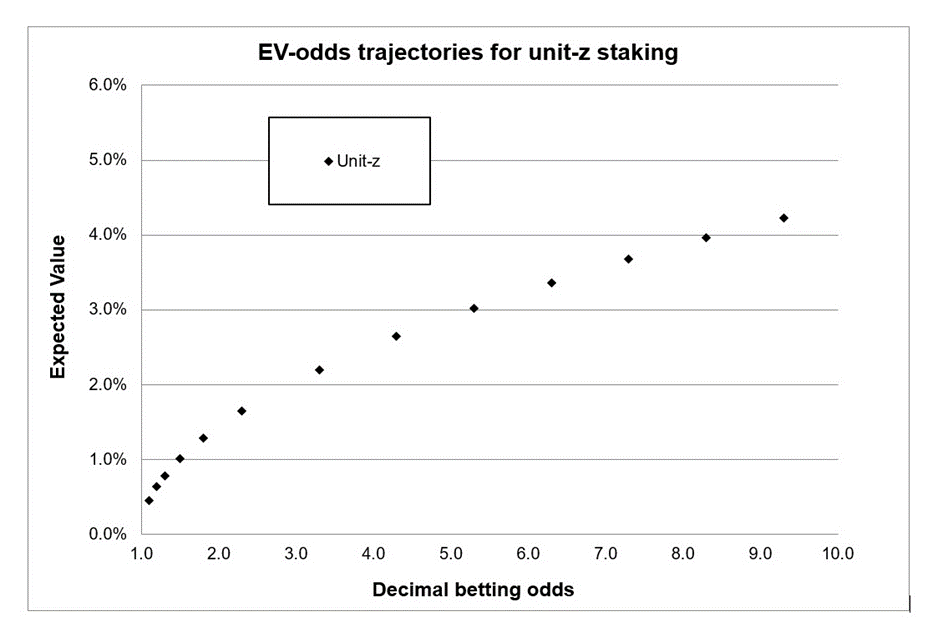
Так как кривая «единицы-Z» довольно точно совпадает с данными из реального мира, давайте будем использовать метод Джозефа в качестве образца для представления действительных результатов.
Как вы считаете, почему кривая принимает именно такую форму? Важно ли это? Что если в данном случае, как и во многих других вопросах ставок на спорт, которые я исследовал, все зависит от доступного игрокам на ставках ожидаемого прироста прибыли (EG)?
Так как размеры банкроллов у разных игроков на ставках могут отличаться, нам понадобиться использовать максимальный ожидаемый прирост прибыли (MEG) для сравнения значений доступного EV при различных коэффициентах.
Если мы рассчитаем MEG для одной из точек данных «единицы-z», а затем составим график линии постоянного оптимального значения EG (LOCO EG) для того же диапазона коэффициентов, который использовался в первой диаграмме, то получится результат, представленный ниже:
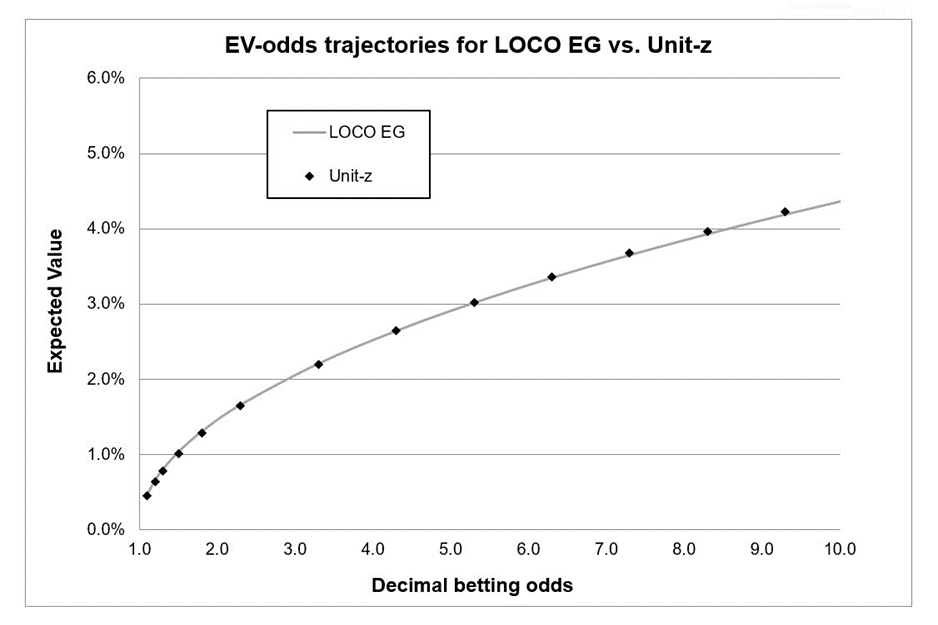
Он полностью совпадает с «единицей-z». Взаимосвязь между EV с любыми заданными коэффициентами и EV с равными суммами денег становится куда более простой для понимания, если для расчетов и составления графика мы будем использовать дробные коэффициенты, а не десятичные:
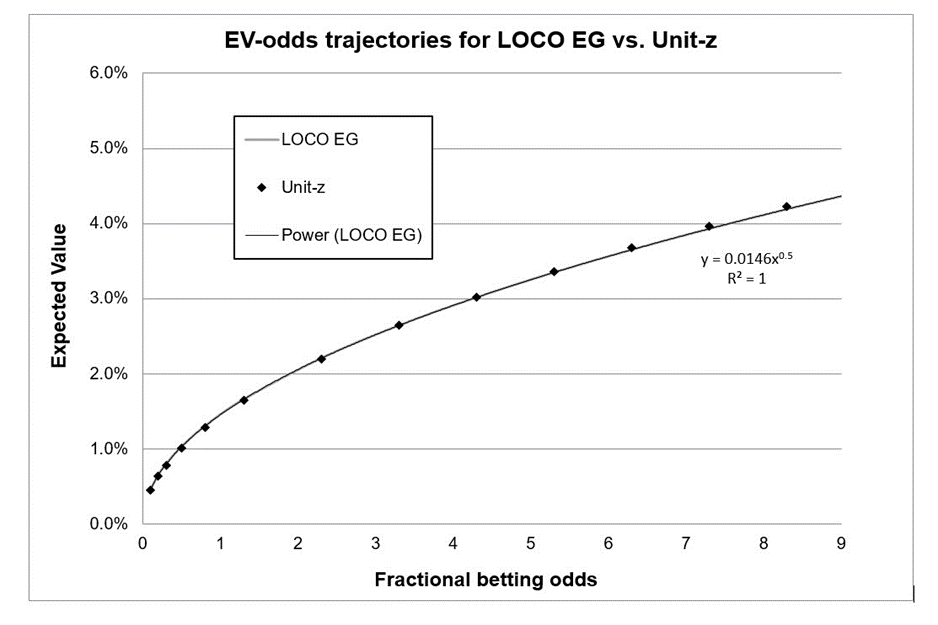
Черная линия тренда, представляющая собой степенную функцию (LOCO EG), на графике выше идеально совмещается с кривой LOCO EG. Так как ось Y этого графика представляет собой EV или преимущество, а ось X – дробные коэффициенты (b), то формула для преимущества (e) для нашей кривой будет выглядеть так:
e = 1,46 % * √b
Откуда взялись 1,46 %? Это значение соответствует ожидаемому преимуществу для равномерных денежных линий в наборе данных, который использовался Бухдалем для задания переменных в формуле «единицы-z». Если вам необходимо всего лишь рассчитать MEG с заданными коэффициентами, которая будет соответствовать варианту с равномерными суммами денег, то можно весьма быстро вывести формулу для вашего ожидаемого преимущества. Стоит начать с использования аппроксимации для MEG:
MEG = преимущество2 / (2 * коэффициенты)
Сумма средств «преимущество в квадрате, деленное на удвоенные коэффициенты» обычно оказывается незначительной, так как она определяет медианное изменение вашего общего банкролла на основании всего одной ставки. Да, это очень удобный инструмент, ведь задав в этой формуле одинаковое значение для всевозможных коэффициентов, мы можем вывести ту формулу, которая будет соответствовать нашей кривой «единицы-z»:
MEG = преимущество2 / (2 * коэффициенты) = преимущество02 / (2 * 1)
e2 / 2b = e02 / 2
e2 = e02b
e = e0√b
e = 1,46 % * √b
Определим переменные:
e = преимущество или EV при заданных коэффициентах
e0 = преимущество или EV при равных суммах денег
На что же указывают полученные результаты? В рамках набора данных из 55 000 точек наилучшая из доступных на рынке линий предоставила игрокам на ставках то же значение MEG, которое предоставляется линией Pinnacle без маржи, какими бы ни были действительные предлагаемые коэффициенты.
Фавориты, аутсайдеры и наиболее очевидные варианты для ставок обладают одинаковым потенциалом для увеличения банкролла, если вы сумеете разместить ставку на наиболее выгодную линию до ее исчезновения и выберете оптимальную сумму денег.
Является ли репрезентативной для всех видов спорта та сокровищница с данными о европейском футболе, которую использовал Джозеф?
Ответ на этот вопрос станет ключевым, ведь если он окажется положительным, мы сможем с легкостью корректировать наши ожидания в отношении выгоды, получаемой от различных значений действительных коэффициентов, используя ожидаемое значение ROI при равных коэффициентах. В этом случае мы сможем выбирать соответствующий размер ставки и использовать преимущество оптимальным образом, не вкладывая в ставку чересчур больших сумм.
Расчет ставок «корня-единицы»
Для того чтобы размещать оптимальную сумму в зависимости от значений LOCO EG, необходимо вспомнить избитую мантру о критерии Келли: размер ставки должен предоставлять преимущество над коэффициентами.
Если мы запишем простое уравнение Келли следующим образом и заменим нашу оценку преимущества при равных суммах денег, мы получим другое весьма простое равенство:
f = преимущество / коэффициенты
f = e / b
f = e0√b / b
f = e0 / √b
Так как оптимальная доля для ставок при равных суммах денег, f0, равна e0, то формула приобретает следующий вид:
f = f0 / √b
Говоря другими словами, чтобы разместить сумму, которая при текущих коэффициентах предоставит вам такое же значение EG, которое вы получили бы на подобном рынке со ставками равных сумм денег, просто разместите ставку, размер которой будет соответствовать ставке равной суммы денег, поделенной на квадратный корень коэффициентов.
Вот почему я называю эту новую технику методом размещения ставок «корня-единицы».
Предположим, что вы собирались размещать ставки величиной в одну единицу на рынках тоталов и форы для НБА, однако заметили хорошее предложение на рынке денежных линий, согласно которому «Пистонс» обыгрывает «Сиксерс» в завтрашнем матче с коэффициентами +400 (5,0 в десятичной форме), – что делать в этом случае?
Вам следует разместить в виде ставки одну единицу, деленную на √4. То есть вы размещаете половину привычной ставки. Теперь предположим, что выгодная ставка на «Сиксерс» обладает коэффициентами –400 (1,250 в десятичной форме).
Тогда следует разместить единицу, деленную на √0,25, то есть две привычных ставки. Так как нет никакой необходимости в точном определении подобных значений (а еще можно выглядеть слишком умным игроком, размещая суммы вроде 103,58 $), я предлагаю использовать в качестве руководства таблицу ниже:
| Американские коэффициенты | Десятичные коэффициенты | Итоговые дробные коэффициенты | Размещаемые единицы |
| –1000 | 1,100 | 1 / 10 | 3,00 |
| –600 | 1,167 | 1 / 6 | 2,50 |
| –400 | 1,250 | 1 / 4 | 2,00 |
| –200 | 1,500 | 1 / 2 | 1,40 |
| –110 | 1,909 | 10 / 11 | 1,05* |
| +100 | 2,000 | 1 | 1,00 |
| +200 | 3,000 | 2 | 0,70 |
| +400 | 5,000 | 4 | 0,50 |
| +600 | 7,000 | 6 | 0,40 |
| +1000 | 11,000 | 10 | 0,30 |
* Если хотите, можно разместить 1,1 единицы, чтобы выиграть 1 единицу для упрощения подсчетов.
Сделайте копию этой таблицы и закрепите ее рядом с монитором при необходимости.
Если вы уверены в своей способности находить преимущества при различных коэффициентах, этот метод поможет вам быстро определять размер ставки подобным критерию Келли способом, при этом вы будете корректировать результат в зависимости от уровня приемлемого риска.
Помните: размещать ставки методом «корня-единицы» можно для любой доли критерия Келли, которая вас устраивает. С помощью метода вы просто сможете поддерживать одинаковое соотношение рисков и наград для любых коэффициентов ставок.
Зарегистрируйтесь уже сегодня и начните размещать ставки на любимые виды спорта, воспользовавшись выдающимися коэффициентами Pinnacle.

